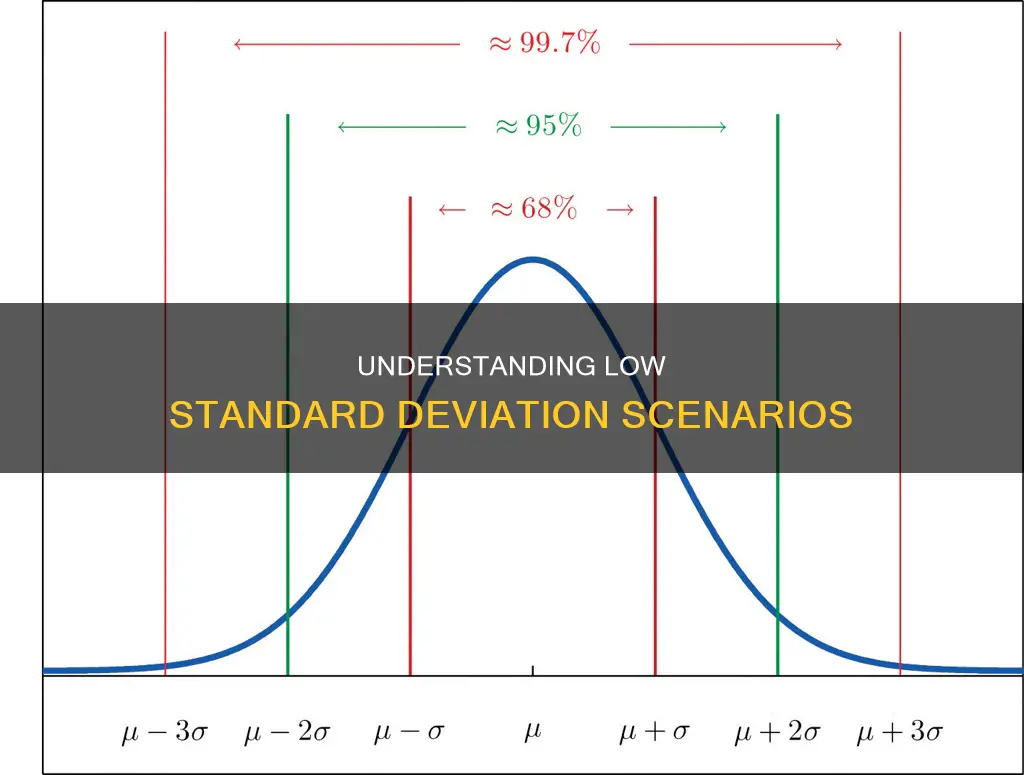
Standard deviation is a statistical measurement that describes how dispersed a set of data is. It is often used in finance and investing to assess risk and volatility. A low standard deviation indicates that data points are clustered tightly around the mean, while a high standard deviation suggests that data points are spread out. There is no universal threshold for a low standard deviation as it depends on the context and type of data being analysed. For example, a standard deviation of $12,000 in house prices may be considered low, while a standard deviation of $480,000 in income tax collected by different countries would be considered high. In the context of stocks, a low standard deviation indicates stable returns, while a high standard deviation suggests higher risk and uncertainty.
| Characteristics | Values |
|---|---|
| Data points | Close to the mean (less variability) |
| Data values | Tightly packed together |
| Coefficient of Variation (CV) | Below 1 |
| Finance & Investments | More stable returns |
| Machine Learning | May require normalization |
| Quality Control & Science | Reliable measurements |
Explore related products
What You'll Learn
- There is no cut-off value for a low standard deviation
- A low standard deviation indicates data clustered around the mean
- A low standard deviation can indicate a stable investment
- A low standard deviation may require normalisation in machine learning
- A low standard deviation can indicate reliable measurements in science

There is no cut-off value for a low standard deviation
There is no single number that can be used to determine whether a standard deviation is "low" or "high". This is because the standard deviation is dependent on the context of the data being analysed. For example, a professor may find that the standard deviation of exam scores is 7.8, while an economist may find that the standard deviation of total income tax collected by different countries is $1.2 million. The standard deviation in the second scenario is much higher, but this is because the values being measured are considerably higher.
When determining whether a standard deviation is low, it is often compared to the mean of the dataset. A coefficient of variation (CV) is a way to measure how spread out values are in a dataset relative to the mean. It is calculated as the ratio between the standard deviation and the mean. The higher the CV, the higher the standard deviation relative to the mean. In general, a CV value greater than 1 is considered high.
In finance and investments, a low standard deviation indicates more stable returns, while a high standard deviation indicates a riskier investment. For example, a stable blue-chip stock will have a low standard deviation, while a volatile stock will have a high standard deviation. In machine learning, a low standard deviation in feature values may require normalisation, while a high standard deviation may require outlier handling. In quality control and science, a low standard deviation indicates reliable measurements, while a high standard deviation indicates inconsistent results.
When comparing different datasets, the standard deviation can be used to determine which dataset has the lowest variation. For example, if a professor administers three exams and calculates the standard deviation of scores for each, they can determine which exam had the most closely packed scores and which had the most spread out scores.
Gaining Power: Constitutional Constraints and Strategies
You may want to see also

A low standard deviation indicates data clustered around the mean
Standard deviation is a statistical measurement that describes how dispersed a set of data is. It is often used to compare data points to the mean of all data points, indicating whether the data points are in close proximity to the mean or spread out. A low standard deviation indicates that the data points are tightly clustered around the mean, while a high standard deviation suggests that the data points are more spread out.
The concept of a low standard deviation is particularly relevant in various contexts, such as finance and investments. In investing, for example, a low standard deviation in the annual rate of return indicates stable and less volatile returns. On the other hand, a high standard deviation signifies riskier investments with greater fluctuations in price. This information is crucial for analysts, portfolio managers, and advisors when assessing the risk associated with different investments.
In machine learning, a low standard deviation in feature values may require normalisation, while a high standard deviation may necessitate outlier handling. Additionally, in quality control and science, a low standard deviation indicates reliable measurements, whereas a high standard deviation suggests inconsistent results.
It is important to note that there is no universal cutoff value for a "low" standard deviation. The interpretation of a low or high standard deviation depends on the specific context and the type of data being analysed. For instance, when comparing exam scores, a standard deviation of 7.8 would be considered low, while a standard deviation of $1.2 million in income tax data would be considered high due to the higher values in the latter dataset.
To summarise, a low standard deviation indicates that data points are closely packed together and clustered tightly around the mean. This concept is valuable in various fields, including finance, machine learning, and quality control, as it provides insights into the stability, reliability, and consistency of the data being analysed.
The Constitution: Brennan's Summary
You may want to see also

A low standard deviation can indicate a stable investment
Standard deviation is a statistical measure of how far a variable, such as an investment's return, moves above or below its average (mean) return. It is a measure of volatility and risk.
When it comes to investments, a low standard deviation indicates that prices are more stable, and therefore the investment comes with less risk. This is because the data points are closer to the mean, resulting in less variability.
For example, consider two stocks. Stock A has an average return of 10% with a standard deviation of 20 percentage points. Stock B has an average return of 12% but a higher standard deviation of 30 percentage points. Despite Stock B's higher average returns, an investor may choose Stock A as the safer option because Stock B's additional 2% return is not worth the additional 10% standard deviation (greater risk).
It is important to note that risk is not necessarily negative in the investment world. The riskier the investment, the greater the potential payout. Standard deviation is a useful tool for investors to assess the risk level of an investment and match it to their own risk tolerance.
While standard deviation is a widely used metric, it is not the only measure of investment risk. Other measures such as the Sharpe ratio, beta, and alpha are also used to determine whether an asset is too risky or not risky enough for an investor's preferences.
In summary, a low standard deviation can indicate a stable investment because it suggests that the data points are closely packed together, resulting in less volatility and a lower risk of significant price fluctuations. However, it is important to consider other factors and metrics when making investment decisions.
Upholding the Constitution: A Judge's Sworn Duty
You may want to see also
Explore related products
$60.51 $79

A low standard deviation may require normalisation in machine learning
There is no cut-off value for what is considered a "low" standard deviation. This is because the standard deviation of a set of data points depends on the type of data and the context in which it is being used. For example, a standard deviation of $1.2 million would be considered high when compared to a set of exam scores, but not when compared to the total income tax collected by different countries.
In machine learning, a low standard deviation in feature values may require normalisation. This is because machine learning algorithms are often trained with the assumption that all features contribute equally to the final prediction. However, this assumption fails when the features differ in range and unit, which affects their importance.
Normalisation is a feature scaling technique that transforms the range of features to a standard scale, ensuring uniformity in the numerical magnitudes of features. This avoids the domination of features with larger values compared to other features or variables. For example, a variable that ranges between 0 and 1000 will outweigh a variable that ranges between 0 and 1 if they are not standardised to the same scale.
There are various normalisation techniques, including min-max scaling, z-score normalisation, decimal scaling, and log scaling normalisation. Z-score normalisation, also known as standardisation, involves transforming data to have a mean of 0 and a standard deviation of 1. This is particularly useful when dealing with algorithms that assume normally distributed data, such as many linear models. Other normalisation techniques, such as robust scaling normalisation, are useful when working with datasets that have outliers.
Recognizing Mental Health Emergencies: Signs and Symptoms
You may want to see also

A low standard deviation can indicate reliable measurements in science
Standard deviation is a statistical measurement that is used to indicate how dispersed a set of data is. It is a way to quantify the amount of variation or dispersion of a set of data values from the mean or average. In other words, it measures how much each data point differs from the mean.
A low standard deviation indicates that the data points are clustered closely around the mean, suggesting that the data values are relatively close to one another. In this case, the variation in the data set is small, and the data points are not spread out widely. Conversely, a high standard deviation indicates that the data points are spread out and vary significantly from the mean, resulting in a larger variation within the data set.
When it comes to determining what constitutes a "low" standard deviation, it's important to understand that there is no universal cutoff value. The interpretation of a low or high standard deviation depends on the context and the type of data being analysed. For example, in finance and investments, a low standard deviation in the annual rate of return of an investment indicates stable and consistent returns, while a high standard deviation suggests higher risk and volatility. In this context, a stable blue-chip stock typically exhibits a lower standard deviation, indicating less price fluctuation.
In the field of science, a low standard deviation can indeed indicate reliable measurements. When conducting experiments or collecting data, scientists aim for consistency and accuracy. A low standard deviation suggests that the measurements are tightly grouped together, indicating a high degree of precision and reproducibility. For example, in particle physics, a "5 sigma" level, corresponding to a very low probability of a random fluctuation, is often used as a standard for declaring a discovery.
It's worth noting that the concept of a “good” or “bad” standard deviation is not universally applicable. Standard deviation simply describes the spread of data points. However, in certain contexts, a high standard deviation may be desirable. For instance, in machine learning, a high standard deviation may indicate the need for outlier handling, while a low standard deviation may require normalization of feature values.
The Police Force: A Constitutional Right?
You may want to see also
Frequently asked questions
Standard deviation is a statistical measurement that describes how dispersed a set of data is. It compares each data point to the mean of all data points and indicates whether the data points are in close proximity to the mean or whether they are spread out.
There is no cut-off value for what is considered a "low" standard deviation because it depends on the type of data you're working with. A low standard deviation indicates that data points are very close to the mean, whereas a larger standard deviation indicates data points are spread further away from the mean.
A coefficient of variation (CV) is a way to measure how spread out values are in a dataset relative to the mean. The CV is the ratio between the standard deviation and the mean. The higher the CV, the higher the standard deviation relative to the mean. A CV value greater than 1 is often considered high.
In finance and investing, a low standard deviation indicates more stable returns, while a high standard deviation indicates a riskier investment. For example, a stable blue-chip stock will have a low standard deviation, while a volatile stock will have a high standard deviation.











































