Large sample sizes are integral to scientific research and publishing as they provide more accurate and reliable results. The concept of a large sample size is relative and depends on the topic of study. In medicine, for instance, large studies on common conditions like heart disease may enrol tens of thousands of patients. In statistics, a sample size of 30 is often considered the minimum for applying the Central Limit Theorem, which states that as sample size increases, the sample mean gets closer to the population mean. According to Lin, Lucas, and Shmueli (2013), sample sizes over 10,000 cases are considered large. However, in some cases, sample sizes of 5,500 may be considered sufficiently large.
| Characteristics | Values |
|---|---|
| Relative nature of large sample size | The concept of a large sample size is relative and depends on the topic being studied. |
| Sample size for academic research | Academic publishers seek manuscripts with large sample sizes to ensure reliability and certainty. |
| Sample size for medical research | Large studies in medicine may enroll tens of thousands of patients, while specialty journals may consider studies with hundreds of patients as large. |
| Central Limit Theorem | According to the Central Limit Theorem, a sample size of at least 30 is considered sufficient for the sample mean to approximate a normal distribution. |
| Effect size | Cohen's interpretation of effect size suggests that 0.1 is a small effect, 0.3 is a medium effect, and 0.5 is a large effect. |
| Sample size for surveys | A sample size of 1000+ is typically used for surveys with yes/no answers. |
| Sample size for statistical significance | A sample size of 5,500 is considered sufficiently large to achieve statistical significance. |
Explore related products
What You'll Learn

The Central Limit Theorem
The CLT is often used in conjunction with the law of large numbers, which states that the average of the sample means will come closer to equalling the population mean as the sample size grows. This can be extremely useful in accurately predicting the characteristics of very large populations. For example, an investor may use the CLT to study a random sample of stocks to estimate returns for a portfolio.
The CLT is also useful when analysing large data sets because it allows for easier statistical analysis and inference. For instance, investors can use the CLT to aggregate individual security performance data and generate a distribution of sample means that represent a larger population distribution for security returns over some time.
The CLT can be applied when the sample size is equal to or greater than 30, which is considered the minimum for applying the theorem. This is because n=30 is when the sample mean's distribution becomes close enough to a normal distribution, visually speaking. However, if the data is skewed or has big outliers, a larger sample size may be necessary.
The CLT does not have a formula for its practical application. Instead, its principle is simply applied. As the sample size increases, the sample distribution will approximate a normal distribution, and the sample mean will approach the population mean.
The Tennessee Constitution: A Concise Word Count
You may want to see also

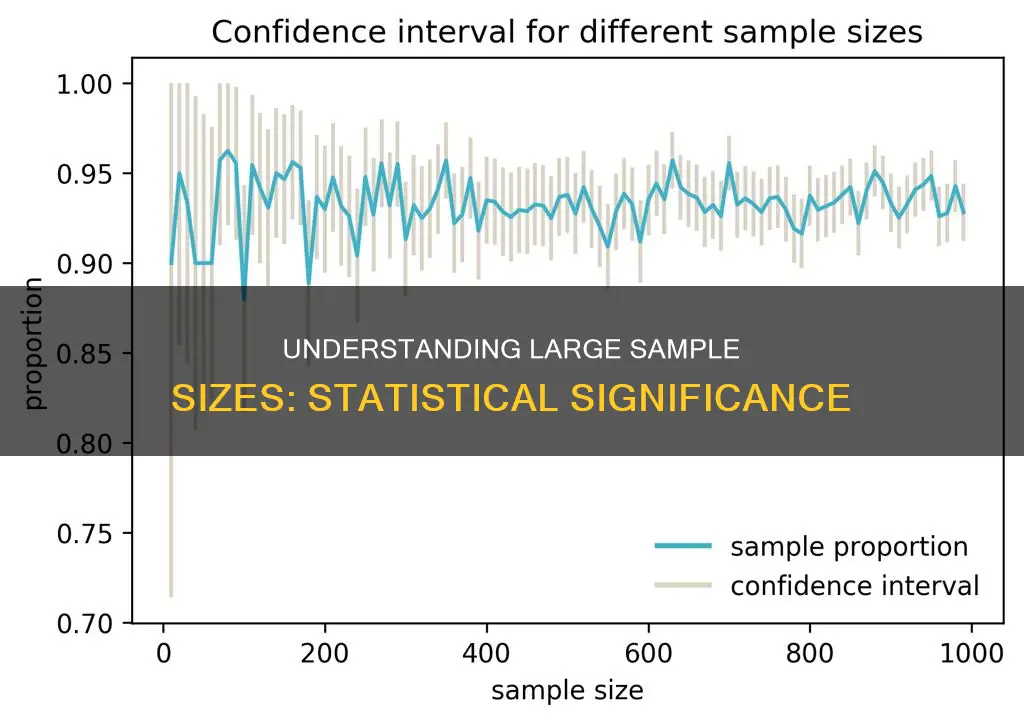
Sample size and accuracy
The concept of a large sample size is relative and depends on the topic being studied. In medicine, for instance, large studies on common conditions like heart disease or cancer may enrol tens of thousands of patients, while for specialty journals, a few hundred patients may constitute a large study.
In statistics, a commonly cited "rule of thumb" is n=30, which is significant for the Central Limit Theorem. According to this theorem, as sample size increases, the sampling distribution of the sample mean approximates a normal distribution, regardless of the original data distribution. While n=30 is a good target, in practice, a sample size of 29 or 31 would also suffice.
The Central Limit Theorem is often used with the law of large numbers, which states that as the sample size grows, the sample mean gets closer to the population mean. This can be useful in accurately predicting characteristics of large populations and does not require the entire population to be studied.
Larger sample sizes are generally desirable as they provide more accurate average values, help identify outliers, and reduce the margin of error. They also help researchers control the risk of reporting false negatives or false positives.
However, it's important to note that not all research questions require massive sample sizes. When determining the appropriate sample size for a study, it's crucial to consider factors such as the type of data, the level of confidence desired, and the specific hypothesis being tested. Working with experts in statistics and study design can help ensure that the sample size is sufficient to provide highly accurate answers.
While a larger sample size often improves accuracy, it is not the only factor at play. The quality and representativeness of the samples are also critical. For example, in a poll or survey, the way people are selected can introduce bias, affecting the accuracy of the results. Thus, a large sample size does not guarantee accuracy, but it can help improve it when combined with careful study design and sampling techniques.
Understanding the Declaration of Independence and US Constitution
You may want to see also

Big data and significance
The concept of a large sample size is relative and context-dependent. In statistics, a sample size of n = 30 is often considered a "magic number" or a rule of thumb for the Central Limit Theorem, which states that as the sample size increases, the sampling distribution of the sample mean approaches a normal distribution. However, the appropriateness of a sample size depends on various factors, including the nature of the data, the research objectives, and the statistical tests being employed.
Big data, on the other hand, typically involves enormous volumes of data that surpass the capabilities of conventional software tools to manage and analyse within a reasonable timeframe. It is characterised by the three Vs: volume, variety, and velocity. Big data deployments often encompass terabytes, petabytes, or even exabytes of data points, and its analysis may necessitate massively parallel software running on numerous servers.
The significance of big data lies in its potential to offer valuable insights and inform decision-making. Organisations across various sectors, including healthcare, finance, retail, and government, leverage big data for a range of applications. For example, big data helps healthcare providers identify disease signs and risk factors, aids financial firms in risk management, assists retailers in personalised marketing, and supports government initiatives in areas such as emergency response and smart city development.
The utilisation of big data in academic research, however, presents certain challenges. One notable issue is the guaranteed statistical significance that arises when using large samples. This necessitates reporting practical significance through effect size measures. Effect size quantifies the magnitude of an effect and provides context for interpreting statistical results. Various effect size metrics are employed, such as Cohen's cut-off points, which categorise effects as small (0.1), medium (0.3), or large (0.5).
In summary, the concept of a large sample size varies depending on the context and the capabilities of analytical tools. Big data represents a significant advancement, offering unprecedented volumes and varieties of data generated and processed at high velocities. Its significance lies in its ability to provide valuable insights, improve decision-making, and drive innovation across industries. However, when utilising big data in research, it is crucial to consider both statistical and practical significance to ensure meaningful interpretations of the results.
The Constitution's Judicial Power: What's Specified?
You may want to see also
Explore related products
$89 $109.99

Effect size metrics
Effect size is a fundamental component of statistics that measures the magnitude of an effect and indicates the practical significance of a result. It is independent of sample size and is calculated using only the data. Effect size is essential for evaluating the strength of a statistical claim and plays a crucial role in power analyses to determine the necessary sample size for experiments.
In meta-analyses, multiple effect sizes are combined, and the uncertainty in each effect size is used to weigh them, giving more importance to larger studies. The uncertainty is calculated based on the sample size or the number of observations in each group. Effect sizes can be absolute or relative, with larger absolute values indicating stronger effects. Standardized effect size measures are typically used when the metrics of the variables lack intrinsic meaning, such as arbitrary scales in personality tests.
Cohen has proposed interpretations of correlational effect size results, suggesting that 0.1 represents a small effect, 0.3 a medium effect, and 0.5 a large effect. These cut-off points provide a framework for understanding the magnitude of the effect and its practical significance.
It is important to note that the criteria for a small or large effect size may vary depending on the specific field of research. Therefore, it is advisable to refer to other papers in the same field when interpreting effect sizes. Effect sizes should be calculated before and after data collection to determine the minimum sample size required for sufficient statistical power to detect an effect.
Power Play: Rules Governing the Capitol Explored
You may want to see also

Sample size and precision
Sample size is defined as the number of pieces of information, data points, or patients (in medical studies) tested or enrolled in an experiment or study. The larger the sample size, the more accurate the average values will be. Larger sample sizes also help researchers identify outliers in data and provide smaller margins of error.
In statistics, the rule of thumb for the Central Limit Theorem is n=30, which is the minimum sample size for the sample mean's distribution to approximate a normal distribution. However, the concept of a large sample size is relative and depends on the topic of study. For example, in medicine, large studies investigating common conditions may enrol tens of thousands of patients, while for specialty journals, 'large studies' may include clinical studies with hundreds of patients.
The precision of the results is directly proportional to the sample size. Larger studies provide stronger and more reliable results because they have smaller margins of error and lower standards of deviation. Standard deviation measures how spread out the data values are from the mean, and as the sample size increases, the margin of error decreases.
In addition to sample size, other factors such as the shape of the data distribution, the type of data, and the research question being addressed also play a role in determining the precision of the results. For example, for continuous data with small to moderate skew, a one-sample t-test, and interest in the confidence interval, n=30 would be sufficient. On the other hand, a survey with yes/no answers may require a sample size of 1000 or more.
To determine an adequate sample size for an experiment, researchers must consider the chances of detecting a difference between the groups compared and work with biostatisticians and experts in study design to ensure an accurate answer to their hypothesis. While not all research questions require large sample sizes, many do, and it is advantageous for authors to submit manuscripts based on studies with large sample sizes to achieve highly certain and reliable results.
Compromise: Constitution Ratification's Key
You may want to see also
Frequently asked questions
The concept of a large sample size is relative and depends on the topic being studied. In medicine, for example, large studies on common conditions may enrol tens of thousands of patients. In general, a sample size of 30 is considered the minimum for applying the Central Limit Theorem, which states that as sample size increases, the sampling distribution of the sample mean approximates a normal distribution.
Larger sample sizes provide stronger and more reliable results as they have smaller margins of error and lower standard deviations. This helps researchers identify outliers in data and reduces the risk of reporting false-negative or false-positive findings.
One challenge is that as sample sizes increase, the statistical significance may be guaranteed, but the practical significance may be diminished, requiring the use of effect size measures. Additionally, collecting and analysing large amounts of data can be time-consuming and costly, and may require specialised software or hardware.