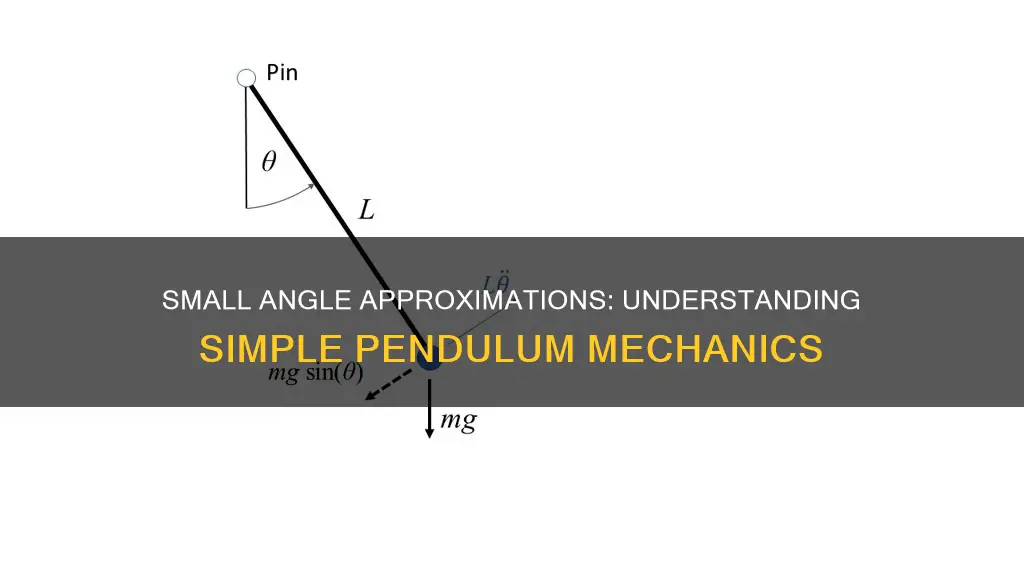
The motion of a simple pendulum is a concept that is relatively easy to describe with basic mathematics. Small angles in a simple pendulum are defined by the small-angle approximation, which states that for small angles of oscillation (typically around 10° or less), the equation of motion can be simplified using the approximation sin(θ)≈θ. This implies that the motion can be modelled as simple harmonic motion (SHM). The small-angle approximation is relevant for both simple and physical pendulums when considering small oscillations, as it simplifies calculations and allows for easier solutions.
| Characteristics | Values |
|---|---|
| Angle | Typically around 10° or less |
| Mathematical formula | T=2π√(L/g) |
| Equation of motion | \(\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin\theta = 0\) |
| Equation of simple harmonic motion | \(\frac{d^2\theta}{dt^2} + \frac{g}{L}\theta = 0\) |
| Simple harmonic solution | \(\theta(t) = \theta_o \cos(\omega t)\) |
| Natural frequency of motion | \(\omega = \sqrt{g/L}\) |
| Behaviour | Does not change for large angles |
| Small-angle approximation | \(\sin\theta\approx\theta\) |
Explore related products
What You'll Learn

The small angle approximation
The motion of a simple pendulum is relatively complicated mathematically. However, simplifying assumptions can be made for small-angle oscillations. The small-angle approximation is a method that assumes that sin(θ) ≈ θ. This is central to all treatments of the simple pendulum as a harmonic oscillator.
The small-angle approximation is needed to understand the behaviour of simple pendulums. The behaviour of the pendulum does not change for large angles; it is simply harder to describe mathematically. The small-angle approximation is used to describe the motion of a pendulum with basic mathematics. The pendulum's angle of motion is described by the variable θ. The angle θ is measured in radians and is the maximum angle between the rod of the pendulum and the vertical.
The small-angle approximation is also used to calculate the period of the motion of a simple pendulum. The period is independent of the amplitude θ0. The period can be calculated using the formula T0 ≈ 2√l, where T0 is the number of seconds between two beats, and l is the length of the pendulum measured in metres.
The small-angle approximation is also used to calculate the exact period of a pendulum for amplitudes beyond the small-angle approximation. This can be done by first inverting the equation for the angular velocity obtained from the energy method and then integrating over one complete cycle. The formula for this is T = 4√(l/2g)∫0θ0(dθ/√(cosθ-cosθ0)), where g is the acceleration due to gravity.
The small-angle approximation is a useful tool for understanding the behaviour of simple pendulums and can be used to calculate various quantities related to the motion of the pendulum. It is a simplification that allows for the analytical solution of the equations of motion for small-angle oscillations.
Syria's Constitution: Israel's Legal Recognition
You may want to see also

The sine of a small angle
The motion of a simple pendulum is relatively easy to describe with basic mathematics for small angles. The small-angle approximation is central to all treatments of the simple pendulum as a harmonic oscillator. This approximation assumes that sin(θ) ≈ θ, where θ is the angle of displacement. In other words, for small angles, the sine of the angle is approximately equal to the angle itself in radians. This approximation allows for the calculation of trigonometric functions like sine, cosine, and tangent with reasonable accuracy.
The small-angle approximation is widely used in mathematics and the physical sciences to simplify equations and make problems more analytically tractable. It is particularly useful in mechanics, electromagnetism, optics, cartography, astronomy, and computer science. For example, in optics, small-angle approximations form the basis of the paraxial approximation. In astronomy, the angular size of distant objects is often only a few arcseconds, making it well-suited to the small-angle approximation.
In the context of a simple pendulum, the small-angle approximation is used to calculate the period of the pendulum by comparing the resulting differential equation with the equation describing simple harmonic motion. This approximation allows for a solution that exhibits simple harmonic motion. The behaviour of the pendulum does not change for larger angles, but the approximation becomes less accurate, making it more challenging to describe mathematically.
The small-angle approximation can be derived using the calculus technique of Taylor series approximation for both sine and cosine. The lowest-order approximation is given by \(f(x) \approx x\), which corresponds to the small-angle approximations for sine and cosine functions. For very small angles (<0.1 radians or 5.7 degrees), the approximation is highly accurate, with a very small error.
The US Occupation: Japan's Constitution Rewrite
You may want to see also

Simple harmonic motion
A simple harmonic oscillator is a system that oscillates with SHM. An example of SHM is an object with mass attached to a spring on a frictionless surface. The object oscillates around the equilibrium position, and the net force on the object is equal to the force provided by the spring. This force obeys Hooke's law. If there is no energy loss in the system, the mass continues to oscillate. However, if there is energy loss, the mass exhibits damped oscillation.
The period of a simple harmonic oscillator is related to the stiffness of the system. A stiffer object has a larger force constant (k), resulting in a smaller period. Additionally, the period depends on the mass of the oscillating system. A more massive system will have a longer period.
Now, a simple pendulum exhibits simple harmonic motion only for small angles. This is because, for small angles, the motion of a pendulum is relatively easy to describe with basic mathematics. The small-angle approximation, sin(θ) ≈ θ, is central to all treatments of the simple pendulum as a harmonic oscillator. The sine of a small angle is essentially equal to the angle, and this approximation allows for a solution that exhibits SHM.
William Paterson's Influence on the US Constitution
You may want to see also
Explore related products

The angle of displacement
Small angles in the context of a simple pendulum refer to the small-angle approximation, which is a mathematical concept used to simplify the equation of motion for a simple pendulum. This approximation states that for small angles of oscillation, typically around 10° or less, the sine of the angle (θ) can be approximated as the angle itself (sin(θ) ≈ θ when θ is in radians). This allows the complex nonlinear motion of the pendulum to be modelled as simple harmonic motion (SHM), making it easier to solve analytically.
The small-angle approximation is central to all treatments of the simple pendulum as a harmonic oscillator. It is based on the idea that the restoring force in a simple pendulum is approximately linear for small angles. This approximation simplifies the calculation of the angular frequency (ω) and allows for similar analyses of both simple and physical pendulums when considering small oscillations.
In the context of a simple pendulum, the small-angle approximation is used to derive the period of oscillation, given by the formula: T=2πgl, where T is the period, l is the length of the string, and g is the acceleration due to gravity. This approximation holds true when the amplitude of angular displacement is small enough, and it allows us to model the motion of the pendulum using basic mathematics.
It is important to note that the behaviour of the pendulum itself does not change for larger angles. The small-angle approximation simply makes it easier to describe and predict the motion mathematically. For larger angles, the equation of motion must remain in its nonlinear form, which requires numerical methods to solve.
Exploring Dimethyl Benzene's Surprising Number of Isomers
You may want to see also

The behaviour of the pendulum
The behaviour of a simple pendulum is a topic that has been extensively studied and modelled using mathematics and physics. The motion of a simple pendulum is often described as simple harmonic motion or SHM. This motion is observed when the angle of oscillation is small, typically around 10° or less. This small-angle approximation simplifies the equation of motion, making it easier to solve analytically.
The small-angle approximation is based on the idea that for small angles, the sine of the angle (θ) can be approximated as the angle itself (sin(θ) ≈ θ when θ is in radians). This allows us to model the motion as simple harmonic motion. For example, if a simple pendulum swings with a maximum angle of 5°, we can apply the small-angle approximation. This approximation is used to derive the period of oscillation, given by the formula: T=2πgl, where T is the period, l is the length of the string, and g is the acceleration due to gravity.
The small-angle approximation is not just relevant to simple pendulums but also to physical pendulums, which are defined as any rigid body that oscillates about a pivot point. By using this approximation, we can analyse the motion of both types of pendulums similarly when the angles are small. This reflects their harmonic motion. The small-angle approximation simplifies the calculation of the angular frequency (ω) for these systems and is often used to describe the behaviour of pendulums as harmonic oscillators.
It is important to note that the behaviour of the pendulum itself does not change for large angles. The mathematics used to describe and predict the motion of real objects is an approximation to make it easier for us to understand. For small angles, the motion of a pendulum is relatively easy to describe with basic mathematics. As the angle of motion becomes larger, the behaviour of the pendulum remains the same, but it becomes more challenging to describe mathematically. This is because the simple mathematical model used for small angles may no longer suffice, and more complex mathematics may be required.
The Supreme Court's Stance on Death Penalty Constitutionality
You may want to see also
Frequently asked questions
A simple pendulum consists of a ball (point-mass) hanging from a string of length L and fixed at a pivot point P.
The small-angle approximation is a mathematical concept where the motion of a pendulum can be modelled as simple harmonic motion (SHM). It assumes that sin(θ) ≈ θ, where θ is the angle of displacement.
Typically, a small angle in a simple pendulum is considered to be around 10° or less. However, some sources suggest that the specific value may vary depending on the specific conditions and parameters of the pendulum.
The small-angle approximation simplifies the equation of motion for a simple pendulum, making it easier to solve analytically. It allows us to describe the motion of the pendulum with basic mathematics and understand its behaviour more easily.