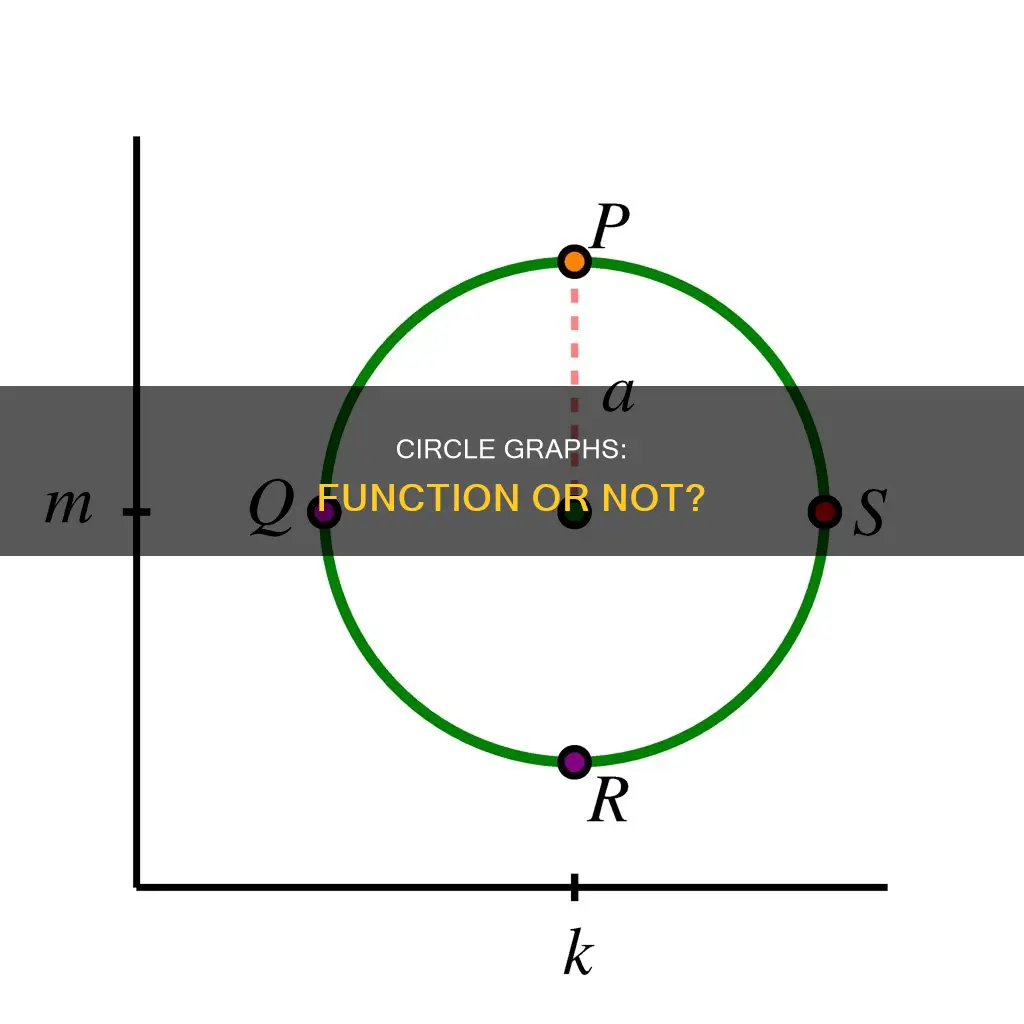
The graph of a circle does not constitute a function. A function is a rule that assigns a member of a domain set to a member of an image set. In other words, for a given input, there can only be one output. A circle, on the other hand, fails the vertical line test, which states that if a vertical line intersects the graph at more than one point, then it is not a function. For example, the equation of a circle, $x^2 + y^2 = 1$, can be rewritten as $y = \pm\sqrt{1-x^2}$, which has two distinct solutions for y for a given x. Therefore, the graph of a circle does not represent a function.
| Characteristics | Values |
|---|---|
| Circle equation | $y2 + x2 = 1 |
| Vertical line test | Fails the test, hence not a function |
| Two possibilities for y | \(y=\sqrt{1-x^2}\) or \(y=-\sqrt{1-x^2}\) |
| Two functions | \(f(x) = \sqrt{1 - x^2}\) or \(f(x) = -\sqrt{1 - x^2}\) |
| Union of functions | A circle |
| Semi-circle | Legitimate function |
Explore related products
What You'll Learn

The circle equation
A circle is not a function because a function is defined by each value in the domain being associated with one point in the codomain. However, a line that passes through a circle intersects the line at two points on the surface.
The equation of a circle provides an algebraic way to describe a circle, given the centre and the length of the radius. The standard equation of a circle with centre (x1, y1) and radius 'r' is:
X - x1)2 + (y - y1)2 = r2
This equation represents the position of a circle on a Cartesian plane. The general form of the equation of a circle is:
X2 + y2 + 2gx + 2fy + c = 0
Where g, f, and c are constants. The general form is used to find the coordinates of the centre of the circle and the radius. The standard form of the equation is easier to understand and provides precise information about the centre and radius of the circle.
The circle can also be represented in polar and parametric forms. The parametric equation of a circle can be written as:
X2 + y2 + 2hx + 2ky + C = 0
Where x = -h + rcosθ and y = -k + rsinθ. The polar form of the equation is similar to the parametric form and is usually written when the circle is centred at the origin.
Qualities Needed to Be President of the United States
You may want to see also

Vertical line test
The vertical line test is a method used to determine whether a given equation represents a function. The test is based on the definition of a function, which states that for a given input, there can only be one output.
The vertical line test works as follows: a vertical line, represented as x = a, is drawn on the graph of a given equation. If the vertical line intersects the graph at only one point, then the equation represents a function. However, if the vertical line intersects the graph at more than one point, then the equation does not represent a function. This is because, for the same x-value, there are now two or more corresponding y-values, which violates the definition of a function.
For example, consider the equation y = \(\sqrt{2x} + 5\). To apply the vertical line test, we choose a vertical line with the equation x = 8. Substituting x = 8 into the equation, we get two points: (8, 1) and (8, 9). Since the vertical line intersects the graph at two points, we can conclude that the equation y = \(\sqrt{2x} + 5\) does not represent a function.
It is important to note that the vertical line test can be applied geometrically or algebraically. Geometrically, the test involves simply drawing a vertical line on the graph of the equation and counting the number of intersection points. Algebraically, the test involves substituting the x-value of the vertical line into the equation and determining if multiple y-values are obtained.
In the context of circle graphs, the vertical line test can be used to demonstrate that a circle does not constitute a function. For example, consider the circle equation x^2 + y^2 = 1. If we draw a vertical line at x = 0.5, we find that the line intersects the circle at two points: (0.5, -\(\sqrt{0.75}\)) and (0.5, \(\sqrt{0.75}\)). Therefore, by the vertical line test, the circle equation does not represent a function.
The Executive: Directly Elected Under the Original Constitution?
You may want to see also

Functions and uniqueness
A function is a rule that assigns a member of a domain set to a member of an image set. In other words, for a given input, there can only be one output. In the context of graphs, this means that a function can be drawn as a curve where no vertical line intersects the curve at more than one point. If a vertical line intersects the curve at more than one point, then the curve represents multiple outputs for a single input, and thus does not represent a function.
The graph of a circle does not pass this "vertical line test." For any vertical line passing through the centre of the circle, there are infinitely many points of intersection with the circle. For example, consider the unit circle with equation $x^2 + y^2 = 1$. If we let $x = 1/2$, then we get two solutions: $y = \pm\sqrt{3}/2$. Thus, the vertical line $x = 1/2$ intersects the circle at two points, and so the graph of the circle does not represent a function.
However, it is important to note that a semi-circle can represent a function. For example, the upper half of the unit circle can be described by the equation $y = +\sqrt{1-x^2}$, and the lower half by $y = -\sqrt{1-x^2}$. Each of these equations represents a unique output for a given input, and so they satisfy the definition of a function.
The concept of "uniqueness" is crucial in the definition of a function. For a function to be well-defined, each input must be assigned a unique output. In the context of graphs, this means that each vertical line should intersect the graph at most once. This ensures that for each value of $x$ (the input), there is only one corresponding value of $y$ (the output). If a graph fails the vertical line test, it represents a relation, which allows for multiple outputs for a single input.
George Washington's Influence on the US Constitution
You may want to see also
Explore related products

Semi-circles as functions
In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a 180° circular arc (or π radians or a half-turn) and has one line of reflection symmetry.
Now, according to the vertical line test, if a vertical line intersects a graph at more than one point, it is not a function. A circle, for example, is not a function because a vertical line drawn through its graph will intersect at two points. However, a semicircle is a legitimate function. The upper half of the semicircle is the positive square root (y = +√(1-x^2)), and the lower half is the negative square root (y = -√(1-x^2)). In other words, for a given input 'x', there are two possible outputs, 'y', which are two different functions, and their union forms the circle.
To illustrate this, consider the circle equation y^2 + x^2 = 1. When solving for 'y', there are two possibilities: y = √(1-x^2) or y = -√(1-x^2). These two functions define the upper and lower halves of the circle, respectively.
It's important to note that functions need to be well-defined, meaning that for a given input, there can only be one output. While a semicircle can be expressed as a function, a circle, in general, cannot because it fails the vertical line test and violates the uniqueness property of functions.
The Constitution's Express Powers: Exploring the Limits
You may want to see also

Functions of two variables
A function is a rule that assigns a member of a domain set to a member of an image set. In other words, for a given input, there can only be one output. A circle, however, fails the vertical line test, which states that if a vertical line intersects the graph of a function at two distinct points, then it is not a function. This is because both points are assigned to the point where the vertical line crosses the x-axis.
However, a semi-circle is a legitimate function. The upper half is the positive square root, and the bottom half is the negative square root. The equation of a circle also cannot be transformed into an equation with only one independent variable. For example, the equation x^2 + y^2 = r^2 cannot be transformed into a univariate function.
A function of two variables is defined similarly to a function of one variable. The main difference is that, instead of mapping values of one variable to values of another variable, we map ordered pairs of variables to another variable. Each ordered pair (x, y) in the domain of the function is mapped to a real number z. Therefore, the graph of the function f consists of ordered triples (x, y, z). The graph of a function z=f(x,y) of two variables is called a surface.
An example of a function of two variables is z=(x, y), where x and y are independent variables, and z is the dependent variable. The domain is the shaded circle defined by the inequality 9x^2 + 9y^2 ≤ 36, which has a circle of radius 2 as its boundary. The range is [0, 6].
Another example of a function of two variables is g(x, y) = sqrt(9 - x^2 - y^2). The domain of g(x, y) is the set of all (x, y) in R^2 such that x^2 + y^2 ≤ 9, and the range is {z in R^2 | 0 ≤ z ≤ 3}. When x^2 + y^2 = 9, we have g(x, y) = 0. Therefore, any point on the circle of radius 3 centered at the origin in the xy-plane maps to z=0 in R^3.
Landowner Voting Rights: A Constitutional Conundrum
You may want to see also
Frequently asked questions
A function is a rule that assigns uniquely to a member of a domain set, a member of the image set. In other words, for a given input, there can only be one output.
One way to determine if a graph constitutes a function is by using the vertical line test. If any vertical line cuts the graph more than once, then it is not a function.
No, a circle does not pass the vertical line test. A vertical line can intersect a circle at two distinct points, and therefore, a circle is not a function.
Yes, a semi-circle is a function. The upper half is the positive square root (y=+$\sqrt{1-x^2}$) and the bottom half is the negative square root (y=-$\sqrt{1-x^2}$).