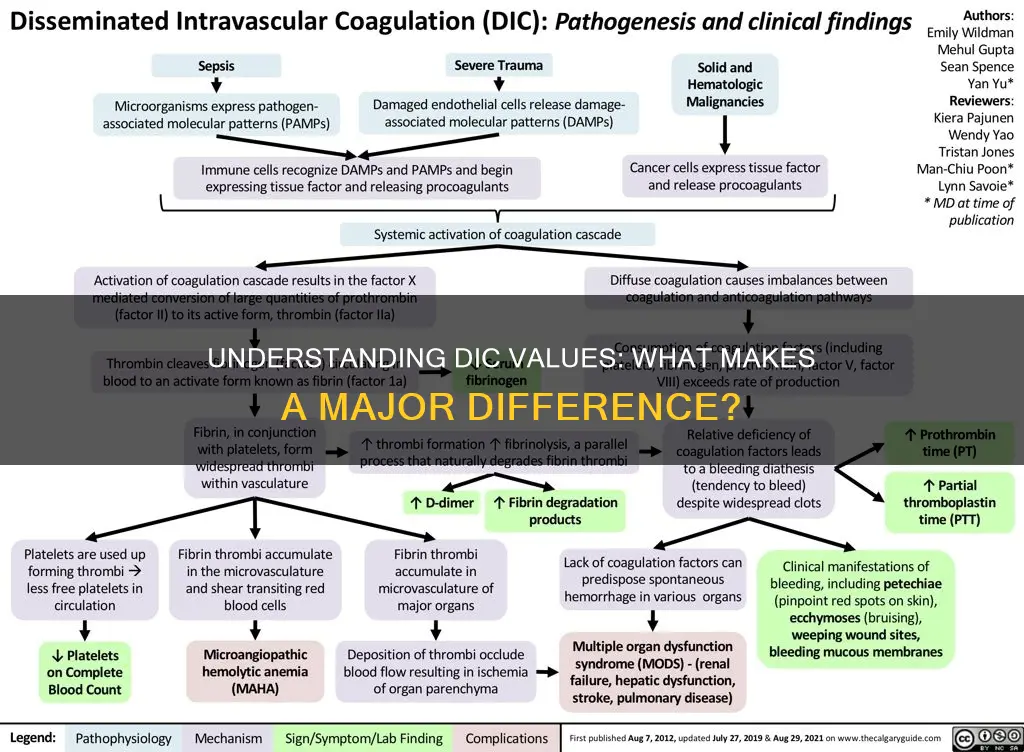
The deviance information criterion (DIC) is a popular method for model selection in the Bayesian community. It is a hierarchical modeling generalization of the Akaike information criterion (AIC) and is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation. While it is widely used, there are increasing concerns regarding its discriminatory performance, especially in the presence of latent variables. This has led to the development of variations of DIC, such as DIC·L and DIC·M, to address specific issues. Given the widespread usage of DIC and its variants, understanding the differences in their values is essential for effective model selection and comparison.
| Characteristics | Values |
|---|---|
| Full Form | Deviance Information Criterion |
| Abbreviation | DIC |
| Type | Hierarchical modeling generalization of the Akaike Information Criterion (AIC) |
| Use Case | Particularly useful in Bayesian model selection problems |
| Calculation | IC = Dbar + 2*pD = -2*E^theta [log(p(y|theta))] + 2*pD |
| First Term | Measure of how well the model fits the data |
| Second Term | Penalty on the model complexity |
| Advantages | Easily calculated from the samples generated by a Markov chain Monte Carlo (MCMC) simulation |
| Disadvantages | Concerns regarding its discriminatory performance, especially in the presence of latent variables |
Explore related products
What You'll Learn
- Deviance Information Criterion (DIC) is a hierarchical modelling generalization of Akaike Information Criterion (AIC)
- DIC is an asymptotic approximation as sample size increases, like AIC
- DIC is only valid when the posterior distribution is approximately multivariate normal
- DIC is widely used for Bayesian model comparison
- DIC is a metric used to compare Bayesian models

Deviance Information Criterion (DIC) is a hierarchical modelling generalization of Akaike Information Criterion (AIC)
The Deviance Information Criterion (DIC) is a hierarchical modelling generalization of the Akaike Information Criterion (AIC). It was introduced in 2002 by Spiegelhalter et al. to compare the relative fit of a set of Bayesian hierarchical models.
Like AIC, DIC selects a model to minimize a plug-in predictive loss. However, unlike AIC, which is based on the log-likelihood function (or deviance) with the maximum likelihood (ML) estimate (MLE) of parameters, DIC is based on the deviance with the posterior mean of parameters. This makes it a Bayesian version of AIC. The posterior mean is obtained through a Markov chain Monte Carlo (MCMC) simulation. AIC requires calculating the likelihood at its maximum over theta, which is not readily available from the MCMC simulation. On the other hand, DIC is easily calculated from the samples generated by the MCMC simulation.
Both DIC and AIC combine a measure of goodness-of-fit and a measure of complexity, both based on the deviance. AIC uses the maximum likelihood estimate, while DIC's plug-in estimate is based on the posterior mean. This is because the number of independent parameters in a Bayesian hierarchical model is not clearly defined, so DIC estimates the effective number of parameters by the difference of the posterior mean of the deviance and the deviance at the posterior mean. This makes DIC a generalization of AIC.
In terms of their advantages, DIC is a widely used measure for Bayesian model comparison, especially after MCMC is used to estimate candidate models. It is also a faster alternative to model evidence, which is considered the gold standard for model selection but is often too computationally demanding. AIC, on the other hand, is a commonly used measure that balances model accuracy and complexity, especially for complex hierarchical models.
The Constitution: Ensuring Public Order and Safety
You may want to see also

DIC is an asymptotic approximation as sample size increases, like AIC
The deviance information criterion (DIC) is a hierarchical modeling generalization of the Akaike information criterion (AIC). It is an asymptotic approximation, which means that it is an estimate that improves as the sample size increases. This is similar to AIC, which also becomes more accurate with larger sample sizes.
DIC is particularly useful in Bayesian model selection problems, where the posterior distributions of the models are obtained through Markov chain Monte Carlo (MCMC) simulation. It is a widely used measure that balances model accuracy against complexity and is considered a faster alternative to other model selection methods.
One of the advantages of DIC is its ease of calculation. It can be directly computed from the samples generated by an MCMC simulation, whereas AIC requires calculating the likelihood at its maximum, which may not be readily available from the MCMC simulation.
Both DIC and AIC are model selection criteria that aim to balance model complexity with how well the model fits the data. They provide measures of model performance that account for model complexity and enable accurate model selection when their underlying assumptions hold true.
While AIC is asymptotically equivalent to cross-validation, it relies on an asymptotic approximation that may not always be valid for a given finite data set. In contrast, DIC assumes that the specified parametric family of probability distributions generating future observations includes the true model, which may not always be the case. Therefore, it is important to consider model assessment procedures when using DIC.
In conclusion, DIC and AIC are both asymptotic approximations that improve with larger sample sizes. They are valuable tools in model selection, each with its advantages and assumptions. DIC is preferred for its ease of calculation and wide applicability, while AIC is favored for its asymptotic equivalence to cross-validation. However, both criteria have their limitations, and it is essential to consider these when interpreting their results.
Executive Orders: Overriding the Constitution?
You may want to see also

DIC is only valid when the posterior distribution is approximately multivariate normal
The deviance information criterion (DIC) is a hierarchical modeling generalization of the Akaike information criterion (AIC). It is a widely used measure that balances model accuracy against complexity. It is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation.
DIC is an asymptotic approximation as the sample size becomes large, like AIC. It is important to note that DIC is only valid when the posterior distribution is approximately multivariate normal. This is a key consideration when applying DIC in practice.
The idea behind DIC is to favor models with a better fit to the data while also considering the complexity of the model. Models with smaller DIC values are preferred over those with larger DIC values. This is similar to AIC, where the model with the smallest AIC value is considered the best among a set of candidate models.
While DIC has its advantages, there are some concerns regarding its discriminatory performance, especially in the presence of latent variables. Additionally, it is worth mentioning that model evidence is considered the gold standard for model selection from a Bayesian perspective. However, its calculation is often viewed as computationally demanding, making DIC a faster and more widely used alternative.
Understanding the Constitutional Status of National Minority Commission
You may want to see also
Explore related products

DIC is widely used for Bayesian model comparison
The Deviance Information Criterion (DIC) is a popular method for model selection in the Bayesian community. It is a hierarchical modelling generalization of the Akaike Information Criterion (AIC) and is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation.
One advantage of DIC over other criteria in Bayesian model selection is that it is easily calculated from the samples generated by an MCMC simulation. AIC, on the other hand, requires calculating the likelihood at its maximum, which is not readily available from the MCMC simulation. This makes DIC a much faster alternative to AIC and other model selection methods.
DIC has been applied in a wide range of fields, including economics, finance, biostatistics, and ecology. For example, in economics and finance, DIC has been used in stochastic frontier models, dynamic factors models, stochastic volatility models, and VAR models. The growth in popularity of DIC among applied researchers can be attributed to its ability to minimize plug-in predictive loss and its detachment from MLE, making it preferable in cases where candidate models are difficult to estimate by ML.
However, there are some concerns regarding the discriminatory performance of DIC, especially in the presence of latent variables. Additionally, the use of the conditional likelihood approach to calculate DIC for latent variable models has been shown to undermine the theoretical underpinnings of DIC. To address these issues, a new version of DIC, DIC·L, has been proposed specifically for comparing latent variable models.
The Chemistry of Mothball Crystals
You may want to see also

DIC is a metric used to compare Bayesian models
The Deviance Information Criterion (DIC) is a metric used to compare Bayesian models. It is a hierarchical modelling generalization of the Akaike Information Criterion (AIC). It is particularly useful for Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation.
DIC is an asymptotic approximation as the sample size becomes large, similar to AIC. It is only valid when the posterior distribution is approximately multivariate normal. The formula for DIC makes some changes to the AIC formula. Firstly, it replaces the maximised log-likelihood with the log-likelihood evaluated at the Bayes estimate. Secondly, it replaces the number of parameters in a model with an alternative correction. The idea is that models with smaller DIC values are preferred to models with larger DIC values.
DIC has been widely used for Bayesian model comparison, especially after MCMC is used to estimate candidate models. It is a popular method for model selection in the Bayesian community and has been applied in a wide range of fields such as biostatistics, ecology, economics, and finance. One advantage of DIC over other criteria in Bayesian model selection is that it is easily calculated from the samples generated by an MCMC simulation.
However, there are some concerns regarding the discriminatory performance of DIC, especially in the presence of latent variables. Additionally, the conditional likelihood approach used in DIC calculations for latent variable models has been shown to undermine the theoretical underpinnings of DIC. To address this, a new version of DIC, called DIC·L, has been proposed specifically for comparing latent variable models.
Checks and Balances: Indirect Elections' Role
You may want to see also
Frequently asked questions
The Deviance Information Criterion (DIC) is a hierarchical modelling generalization of the Akaike Information Criterion (AIC). It is a popular method for model selection in the Bayesian community, particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation.
The DIC is calculated by replacing a maximised log-likelihood with the log-likelihood evaluated at the Bayes estimate and by replacing the number of parameters in a model with an alternative correction. The idea is that models with smaller DIC values are preferred to models with larger DIC values.
There are increasing concerns regarding the DIC's discriminatory performance, especially in the presence of latent variables where there is no unique definition. Furthermore, the conditional likelihood approach used in DIC calculations has been shown to undermine its theoretical underpinnings.
Alternatives to the DIC include Akaike's Information Criterion (AIC), the Bayesian Predictive Information Criterion (BPIC), and Bayesian model evidence. These alternatives aim to address the over-fitting problems and reliability concerns associated with the DIC.