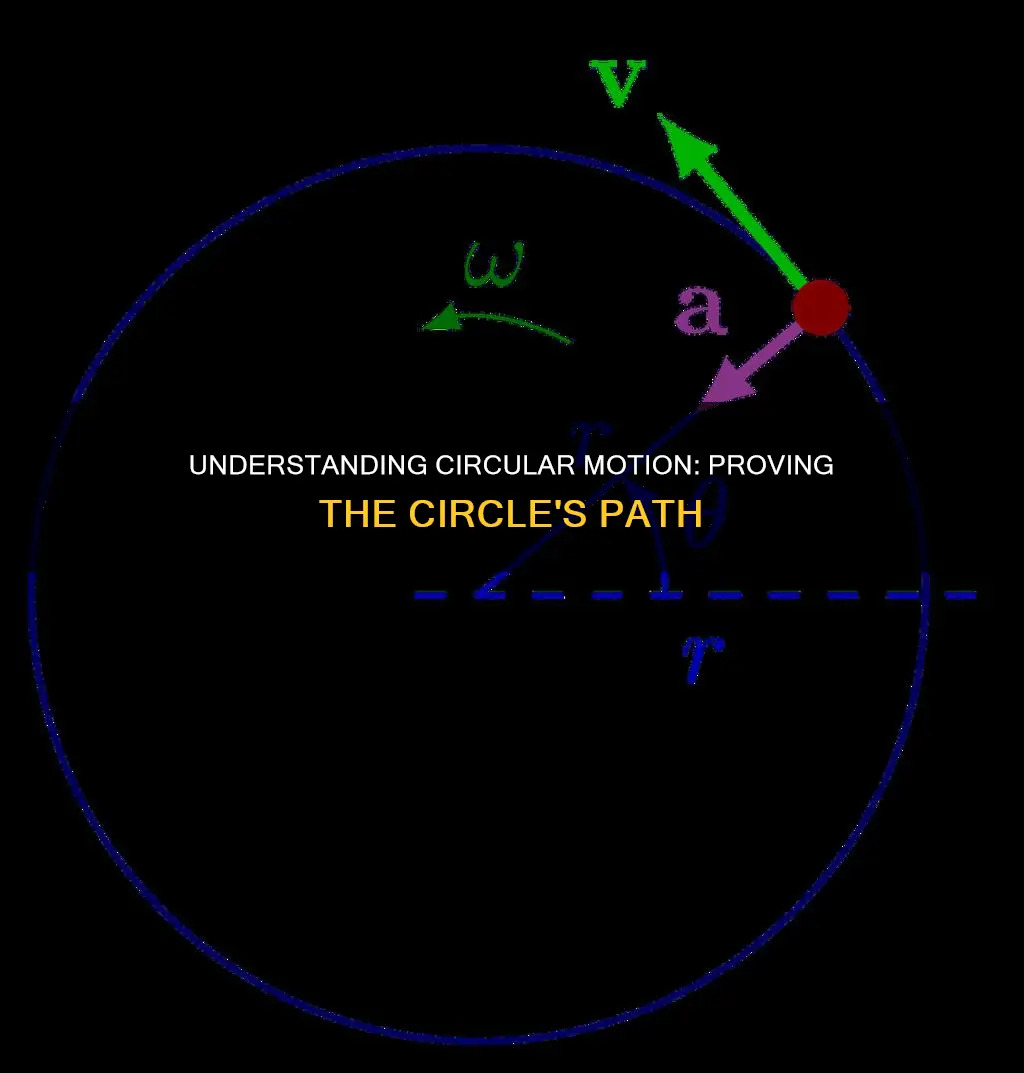
Circular motion is a fundamental concept in physics, describing the movement of an object along a circular path or arc. This motion can be uniform, with a constant rate of rotation and speed, or non-uniform, with a changing rate of rotation. The direction of motion in circular motion is continuously changing, introducing new concepts such as angular displacement, velocity, and acceleration. Centripetal acceleration, directed towards the centre of the circle, is essential to maintaining circular motion, counteracting the natural tendency of objects to move in a straight line. This acceleration results in a centripetal force, which can be provided by gravity, tension, or friction, ensuring the object remains on its circular path. Examples of circular motion are prevalent in everyday life, from a stone swung in a circle by a rope to the rotation of planets around the Sun.
| Characteristics | Values |
|---|---|
| Definition | Circular motion is the movement of an object along the circumference of a circle or rotation along a circular arc. |
| Types | Uniform circular motion (constant rate of rotation and constant tangential speed) and non-uniform circular motion (changing rate of rotation). |
| Examples | Special satellite orbits, ceiling fan blades rotating, a stone swung in circles, a car turning on a curve, an electron moving perpendicular to a magnetic field, a gear turning inside a mechanism, and more. |
| Velocity | Velocity is tangent to the circular path, resulting in no two velocities pointing in the same direction. |
| Acceleration | Acceleration points radially inwards (centripetally) and is perpendicular to velocity. In uniform circular motion, the tangential component of acceleration is zero, while in non-uniform circular motion, it can be positive or negative. |
| Centripetal Force | The force required to maintain circular motion, acting towards the centre of the circle. Examples include gravitational force, tension in a string, and friction. |
| Centrifugal Force | The reaction to centripetal force, equal in magnitude but opposite in direction. Not a "real" force, but rather the manifestation of an object's inertia wanting to move in a straight line. |
| Angular Variables | Angular displacement, angular velocity, and angular acceleration are terms used to describe circular motion. Angular velocity is measured in rad/s. |
| Equations | For a circular path of radius r and angle θ, the distance travelled on the periphery is s = rθ. The centripetal acceleration is given by v^2/r. |
Explore related products
What You'll Learn

Centripetal force
The centripetal force is crucial in keeping an object moving in a circular path. It acts as a constraining force, pulling the object towards the centre of the circle, preventing it from veering off in a straight line. This force is always directed towards the centre, and its magnitude depends on the mass of the object and its velocity. The equation for centripetal force is given by Fc = mv^2/r, where m is the mass, v is the velocity, and r is the radius of the circular path.
Examples of centripetal forces include gravitational force, tension in a string, and friction. In everyday life, the motion of planets around the sun, a stone swinging in a circle at the end of a rope, and a car turning on a curved track all demonstrate centripetal forces at play. In the case of the swinging stone, the tension in the rope provides the centripetal force, keeping the stone in its circular path.
In summary, centripetal force is a fundamental concept in understanding circular motion. It is the force directed towards the centre of a circle that keeps an object moving in a circular path. This force is essential in various natural and man-made systems, from planetary orbits to amusement park rides, showcasing its significance in the physical world.
The Constitution and Gun Background Checks: What's the Deal?
You may want to see also

Angular displacement
The formula for calculating angular displacement is θ = s/r, where θ represents the angular displacement, s is the distance travelled along the circumference of the circle (circular arc length), and r is the radius of the circle. This formula allows us to quantify the amount of rotation an object has undergone in a circular path.
Making the Constitution Work for the People
You may want to see also

Centripetal acceleration
Circular motion is the movement of an object along the circumference of a circle or the rotation of an object along a circular arc. This motion can be uniform, with a constant rate of rotation and a constant tangential speed, or non-uniform with a changing rate of rotation.
The centripetal acceleration experienced by an object in circular motion can be provided by various forces, such as static friction, gravitational force, tension in a string, or friction. For example, in the case of a swinging stone tied to a rope, the centripetal force is supplied by the tension of the rope. Similarly, in a fairground ride, the riders experience centripetal acceleration due to the circular path of the ride.
The magnitude of centripetal acceleration depends on the speed of the object and the radius of the circular path. The sharper the curve and the greater the speed, the more noticeable this acceleration becomes. For instance, when a car turns a corner, the driver and the vehicle experience a sideways acceleration due to the change in direction.
In summary, centripetal acceleration is a fundamental aspect of circular motion, always pointing towards the centre and keeping the object on its circular path. This acceleration is influenced by the speed of the object and the radius of the circle, and it plays a crucial role in understanding the dynamics of circular motion.
Constitution's Two-Party System: Why It's Inevitable
You may want to see also
Explore related products

Velocity
Circular motion is the movement of an object along the circumference of a circle or the rotation of an object along a circular arc. This motion can be uniform, with a constant rate of rotation and a constant tangential speed, or non-uniform with a changing rate of rotation.
The velocity of an object in circular motion is constantly changing, even if the speed remains constant. This is because the direction of the velocity vector changes at each point on the circle. The velocity vector is always tangent to the circular path, meaning no two velocities point in the same direction.
For example, consider a body with a mass of one kilogram, moving in a circle with a radius of one metre, and an angular velocity of one radian per second. The speed of this body is 1 metre per second, but the direction is constantly changing. This change in velocity is caused by an acceleration, which is held constant in magnitude but is always changing in direction. This acceleration, known as centripetal acceleration, points radially inwards towards the centre of the circle.
In the case of non-uniform circular motion, the tangential component of acceleration can take a positive or negative value, whereas in uniform circular motion, it is zero. The acceleration of a particle in circular motion is given by v^2/r, where v is the velocity and r is the radius of the circular path.
The velocity of an object in circular motion is fundamental to understanding the motion's characteristics. By differentiating the position vector of the particle with respect to time, the velocity of the particle can be easily found. This velocity is perpendicular to the position vector and is often referred to as the tangential velocity.
Johnny Appleseed's US Constitution Connection
You may want to see also

Uniform and non-uniform circular motion
Circular motion is the movement of an object along the circumference of a circle or the rotation along a circular arc. This motion can be uniform or non-uniform. In uniform circular motion, the speed of the particle executing circular motion remains constant, and the circle is at a fixed radius. The velocity vector changes direction at each point on the circle, and the radial component of acceleration is always non-zero. The tangential component of acceleration takes a zero value in the case of uniform circular motion.
Uniform circular motion can be observed in the motion of planets revolving around the sun. Although the orbital motion is slightly elliptical, it can be considered circular motion. Other examples include special satellite orbits around the Earth, a ceiling fan's blades rotating around a hub, and a Ferris wheel.
Non-uniform circular motion, on the other hand, involves a change in the magnitude of angular velocity over time. The angular velocity in non-uniform circular motion is not constant, as it depends on the speed and radius of the circular path. The change in direction is accounted for by radial acceleration, also known as centripetal acceleration. In non-uniform circular motion, the normal force does not always point in the opposite direction of weight. Instead, it is the sum of the radial and tangential forces.
Examples of non-uniform circular motion include a car turning on a circular track or a curve in a race track. The effect of friction on the motion of a vehicle on a circular road can be minimised by banking the road, or raising it slightly on the outer end. This helps to reduce the role of friction in the circular motion of the car.
Switzerland's Constitution: A Comprehensive Chapter Guide
You may want to see also
Frequently asked questions
Circular motion is the movement of an object along the circumference of a circle or rotation along a circular arc.
Circular motion can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate of rotation.
Examples of circular motion include special satellite orbits around the Earth, a ceiling fan's blades rotating around a hub, a stone tied to a rope and swung in circles, a car turning through a curve in a race track, and a Ferris wheel.